On the page dealing with Hailstone Signature Analysis mention
was made of the fact that as the hailstone process operates on a number, it will reduce the length of that number
by roughly one digit for each group of 8 Signature Chunks which it calculates for that number. For a single number,
this is very much an approximation, but the Rule-of-8 demonstration program discussed here allows you to execute
the hailstone process on a large group of numbers all of the same length. When the results are averaged over a
group of some thousands of numbers, a quite remarkable result emerges as you will soon see.
The program is called Rule-of-8 and under default conditions it applies the hailstone process to each of 1,000
thirty digit numbers, and as it does so it accumulates the total number of Signature Chunks that were required
to reduce all of these numbers to the final value of one. As a final step, it divides this total by 1,000 to
determine the average number of Signature Chunks required per number.
And here's the payoff! That average always seems to be in the 230s or the 240s. That is to say, very close to 8
times the number of digits in the numbers being processed. Using a greater quantity of numbers (say 10,000) will
generally yield an average of 238 or 239!
For this graphic the Digits per Number was set to 30 and How many Numbers was set to 100,000.
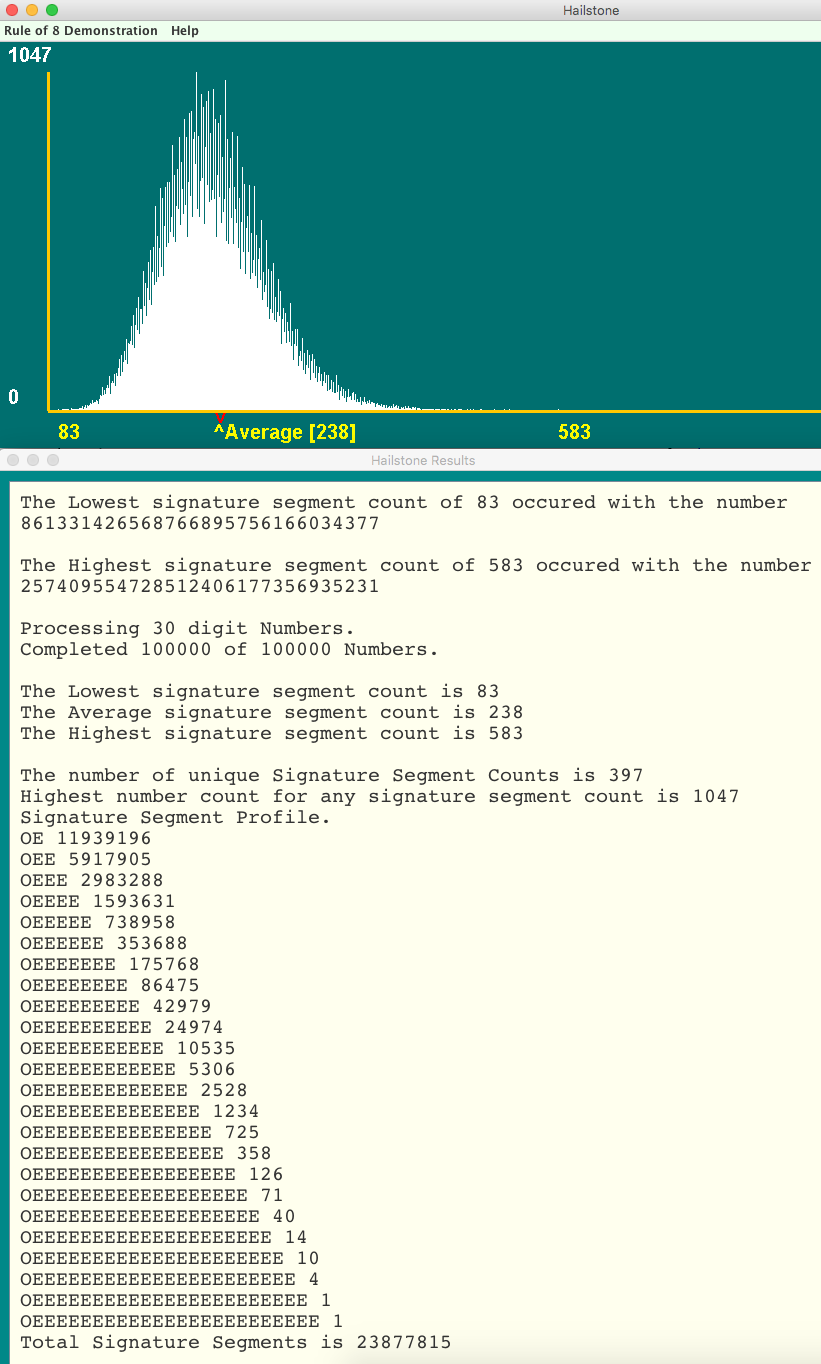 This graphic is in two distinct parts. The top part is a bar graph of the data produced by the batch process, while
the bottom part, labeled Hailstone Results, consists of some explanatory notes pertaining to the graph. The following
notes will try to make clear just what this graphic is saying:-
This graphic is in two distinct parts. The top part is a bar graph of the data produced by the batch process, while
the bottom part, labeled Hailstone Results, consists of some explanatory notes pertaining to the graph. The following
notes will try to make clear just what this graphic is saying:-
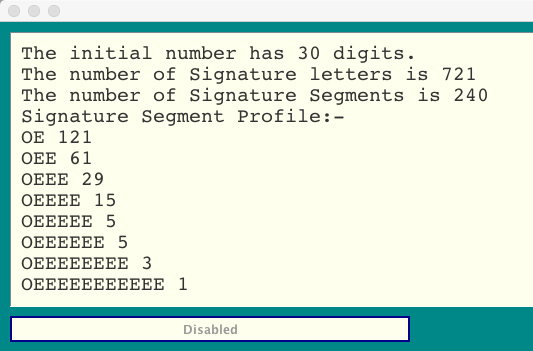 Note that the number of Signature Chunks is 240 which is the number predicted by the Rule of 8 for this
number. That is not an accident ... it's the reason why this number was selected. The Signature Chunk Profile tells
the story of a well behaved number in that the count value of each Chunk type is less than that of the previous
Chunk type. Also, for the first few Chunks at least, the count decreases by a factor close to 2, which is a tendency
suggested by probability considerations.
Here are the results for the number 257409554728512406177356935231:-
Note that the number of Signature Chunks is 240 which is the number predicted by the Rule of 8 for this
number. That is not an accident ... it's the reason why this number was selected. The Signature Chunk Profile tells
the story of a well behaved number in that the count value of each Chunk type is less than that of the previous
Chunk type. Also, for the first few Chunks at least, the count decreases by a factor close to 2, which is a tendency
suggested by probability considerations.
Here are the results for the number 257409554728512406177356935231:-
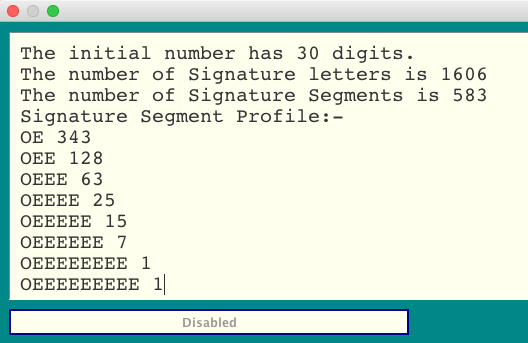 The most outstanding feature here is the high number of OE Chunks in the Signature. Now an OE Chunk is the only type
which actually increases the size of the subject number, so not only does it boost the count of Signature Chunks, it
requires an increased number of other Chunk types to reduce the subject number to its final value of 1.
And here are the results for the number 861331426568766895756166034377:-
The most outstanding feature here is the high number of OE Chunks in the Signature. Now an OE Chunk is the only type
which actually increases the size of the subject number, so not only does it boost the count of Signature Chunks, it
requires an increased number of other Chunk types to reduce the subject number to its final value of 1.
And here are the results for the number 861331426568766895756166034377:-
 Here the number of OE Chunks is only 27 which is less than 10% of the number in the previous case. This, together with
the rather long chains of Es in the last few Chunks listed, conspires to keep the Signature quite short. However it is
a relatively simple matter to design plenty of numbers with much shorter Signatures than this.
For example 222577830099727861365828048213 which has 6 Signature Chunks:-
Here the number of OE Chunks is only 27 which is less than 10% of the number in the previous case. This, together with
the rather long chains of Es in the last few Chunks listed, conspires to keep the Signature quite short. However it is
a relatively simple matter to design plenty of numbers with much shorter Signatures than this.
For example 222577830099727861365828048213 which has 6 Signature Chunks:-
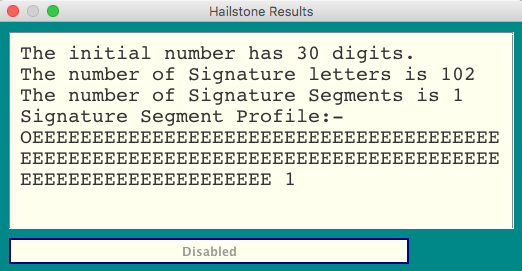
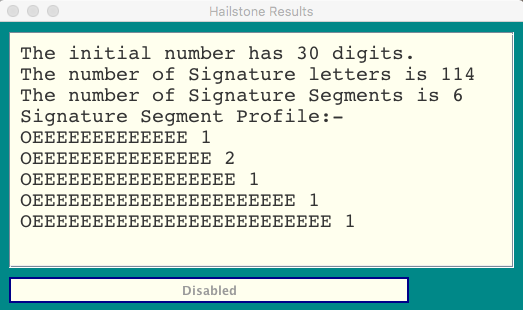 Or even 422550200076076467165567735125 which has just 1 Signature Chunk
Or even 422550200076076467165567735125 which has just 1 Signature Chunk
 In spite of these highs and lows, if you use a large enough batch of numbers when performing a Rule of 8 operation,
(1,000 would do although 10,000 would be better) you will almost invariably find that the Average Number of Chunks per
Signature turns out to be remarkably close to the value predicted by the Rule of 8.
In spite of these highs and lows, if you use a large enough batch of numbers when performing a Rule of 8 operation,
(1,000 would do although 10,000 would be better) you will almost invariably find that the Average Number of Chunks per
Signature turns out to be remarkably close to the value predicted by the Rule of 8.

-
The Lowest and Highest Signature Chunk counts are given along with the numbers being processed at the time.
The fact that 30 digit numbers are being processed is reported, along with a running indicator of how many
numbers have been completed out of the final target of 100,000 numbers.
The graph is immediately recognizable as a "standard" bell curve, with some obvious differences. It is clearly
skewed toward the upper end of the curve, and it is very far from being a smooth curve. It seems that certain
Signature Chunk count values are favored by the hailstone process while others are disadvantaged. Why this is so
may be an interesting question for additional research in the future.
Each point on the x axis of the graph represents a number of Signature Chunks. A vertical bar drawn at any
of these points signifies the fact that one or more numbers treated by the batch process required exactly that
number of Signature Chunks to progress to the final value of 1. The length of the bar indicates the number of
numbers in the batch which required that particular number of Signature Chunks.
The two numbers (83 and 583) printed below the x axis record both the lowest number and the highest number of
Signature Chunks required by the members of the set of numbers to reach the final value of 1. In each of these
cases, the actual 30 digit number which required this number of Signature Chunks is printed as part of the
Hailstone Results.
A red indicator below the x axis points to the location of the Average value of Signature Chunks predicted
by the Rule of 8, and a yellow indicator labeled Average points to the location to the current average for
the numbers processed so far. It is quite entertaining to watch this indicator as the program runs. Initially it
wanders up and down but quickly settles down to a number very close to 240 as predicted by the Rule of 8.
The numbers to the left of the y axis provide a rough indication of how many numbers are associated with each
Signature Chunk count. The maximum number (1047) is also included in the Hailstone Results.
For a discussion about how it happens that the maximum and minimum Signature Chunk counts can depart so far
from the average value, refer to Hailstone Tree Outliers.





The following table contains the results of a series of tests performed by the Rule of 8 function. The columns
contain the following data:-
-
The Number Length is the number of digits in the numbers used for each test in the series. A minimum of
one thousand numbers were processed in each test.
Note that in every case, the Average Number of Chunks per Signature is very close to the (8 times the Number Length) figure predicted by the Rule of 8, and shown in square brackets.
The Highest Number of Chunks per Signature is to be interpreted as the highest number encountered on this run. There will probably be a few higher numbers but these can safely be categorized as outliers.
The Lowest Number of Chunks per Signature is not recorded. This is because there will always be at least one number for any given number length which will have a Signature with only one Chunk.
For example:-
-
2 digit numbers :- 21 and 85
3 digit numbers :- 341
4 digit numbers :- 1365 and 5461
| Number Length |
Average number of Chunks per Signature |
Highest number of Chunks per Signature |
Number Length |
Average number of Chunks per Signature |
Highest number of Chunks per Signature |
|---|---|---|---|---|---|
| 2 | 14 [16] | 43 | 200 | 1602 [1600] | 2201 |
| 3 | 22 [24] | 65 | 300 | 2397 [2400] | 3250 |
| 4 | 31 [32] | 96 | 400 | 3200 [3200] | 3963 |
| 5 | 38 [40] | 129 | 500 | 4001 [4000] | 4857 |
| 6 | 47 [48] | 176 | 600 | 4804 [4800] | 5553 |
| 7 | 55 [56] | 203 | 700 | 5600 [5600] | 6401 |
| 8 | 63 [64] | 218 | 800 | 6397 [6400] | 7458 |
| 9 | 71 [72] | 265 | 900 | 7200 [7200] | 8213 |
| 10 | 78 [80] | 272 | 1000 | 8000 [8000] | 9183 |
| 20 | 158 [160] | 406 | 2000 | 16001 [16000] | 17429 |
| 30 | 238 [240] | 589 | 3000 | 24017 [24000] | 26084 |
| 40 | 319 [320] | 636 | 4000 | 32038 [32000] | 33767 |
| 50 | 398 [400] | 723 | 5000 | 40044 [40000] | 42091 |
| 60 | 479 [480] | 955 | 6000 | 48015 [48000] | 50528 |
| 70 | 559 [560] | 909 | 7000 | 55984 [56000] | 58473 |
| 80 | 638 [640] | 1121 | 8000 | 64013 [64000] | 66737 |
| 90 | 718 [720] | 1118 | 9000 | 72002 [72000] | 74303 |
| 100 | 799 [800] | 1237 | 10000 | 80047 [80000] | 83017 |
In the page Hailstone Signature Analysis it was confidently predicted
that the Rule of 8 would be closely observed as the Hailstone Process is applied to numbers in general. This
table demonstrates very convincingly that the prediction was indeed correct.
The progressive results provided by the Rule of 8 function include a profile of the entire set of Signature
Chunks generated during a batch processing run. The following table was generated during a typical run using one
million 100 digit numbers. The Rule of 8 predicts that the total number of Signature Chunks should be 8 x 100 x
1,000,000 = 800,000,000. The figure that is reported by the program is 799,180,608. This adds quite significantly to
the confidence we can feel in the validity of the Rule.
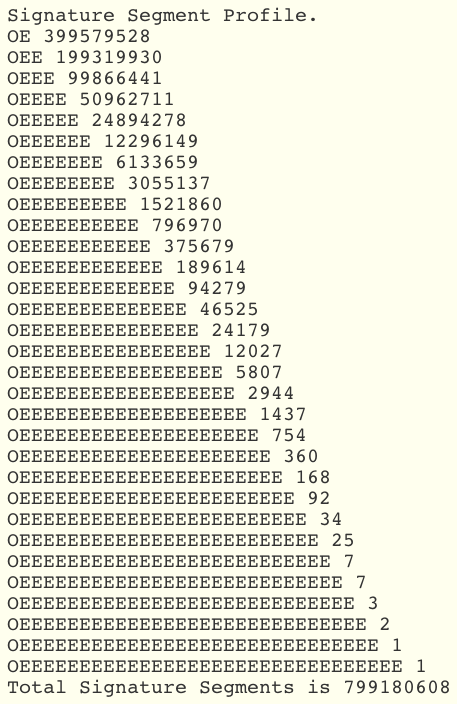 Of equal interest are the numbers of each of the Chunk types. Note that almost exactly half of all the Chunks are of
type OE, and that all of the subsequent types progressively decrease by a factor of 2. This justifies the equal
probability assumptions made in Hailstone Signature Analysis. It is
very comforting to observe this behavior as it adds great support to the Collatz Conjecture. But will it always be the
case? A more pertinent question to ask is why should we imagine that circumstances might arise where it fails? How would
we even begin to define a set of circumstances which would allow it to fail. I will leave that question for others to
ponder.
Of equal interest are the numbers of each of the Chunk types. Note that almost exactly half of all the Chunks are of
type OE, and that all of the subsequent types progressively decrease by a factor of 2. This justifies the equal
probability assumptions made in Hailstone Signature Analysis. It is
very comforting to observe this behavior as it adds great support to the Collatz Conjecture. But will it always be the
case? A more pertinent question to ask is why should we imagine that circumstances might arise where it fails? How would
we even begin to define a set of circumstances which would allow it to fail. I will leave that question for others to
ponder.
